Why my research benefits humanity

I have recently been (successfully) nominated for an international prize for an outstanding doctoral thesis. As a part of the nomination procedure, I was asked to submit a one-page personal note on why my research benefits humanity. I believe that the resulting text should not be only for the eyes of the prize committee, but that it should reach a broader audience. Hopefully, these few paragraphs manage to communicate developments in basic research in an accessible way.

(For anyone too curious, the thesis can be found here.)

 

The advancement of civilizations has been always closely tied to the discovery of new materials and technologies. The possibility to use volcanic ashes to produce concrete was arguably as revolutionary to Roman empire, as the invention of semiconductor-based electronics has been for the modern society in the last century. However, while trial-and-error discovery was sufficient to keep a slow but steady progress millennia ago, recent developments in science require ever finer scrutiny of the laws of nature. Nowadays, major discoveries are usually the fruit of collective effort of wide collaborations, where every member of a team has a narrow but vital role.

I work in the field of condensed matter physics, which aims to find novel materials for technological applications. To describe materials, one needs to refer to some basic constituents of matter. For our purposes, these are ions and electrons. However, the latter must be described in terms of quantum theory, and quantum description of just a single particle can be annoyingly complicated. Explaining a correlated state of 10²⁰ of them seems mind-bogglingly futile. After all, we know that a plethora of phases can emerge from a concoction of atoms, such as magnets (in hard drives), transparent metals (in touchscreens), liquid crystals (in LCDs), or superconductors (in MRI machines) – to mention just some that already found intriguing applications.

Physicists have developed a sequence of approximations that make the description of solids partially tractable: First, solve the problem of a single electron in the potential of all the ions. Second, assume that the behavior of each electron is unaffected by the swarm of the other ones. Finally, with a bit of luck, the interaction between the electrons is treated as a perturbation on top of the non-interacting solution. The last step is notoriously difficult. However, it turns out that even the first step is still not fully understood. Major gaps in our understanding of such simple systems were unearthed by the discovery of topological insulators and semimetals a decade ago.

My research is trying to fill the gaps in the basic description of crystalline solids. Starting with the symmetry of an atomic lattice, I develop the characterization of the single-electron solutions. The result, called a “band structure”, can serve as an input to calculate the material’s transport properties, such as conductivity, thermoelectricity, or the tendency to develop superconducting or magnetic order. However, rather than inspecting specific materials, I use tools of group theory and algebraic topology to classify what kinds of solutions are in principle realizable, and which ones would be mathematically inconsistent. The goal is to obtain a complete list of all the possibilities, making sure that we do not miss any other topological phases this time around.

Admittedly, my mathematical results would not be of much benefit if they were not carried over to the next stage of material design. In collaboration with my colleagues, we attempt to find suitable material candidates for every new kind of solution that we identify. For example, in a joint manuscript Nodal-chain metals, published in Nature, we suggested the existence of a new type of semimetal. We argued that it should exhibit an unusual and strongly anisotropic magneto-electric properties with prospective applications in electronic devices. Although our specific material candidate turned out unsuccessful, the idea was soon picked up by other teams. Since a few months ago, the nodal-chain feature has been experimentally confirmed in TiB₂. In such a meandering way, progressing with small but thoughtfully chosen steps, me and my colleagues work to bring humanity novel materials for future technologies.

Making of a bond

Why doesn’t the negatively charged electron in hydrogen atom fall onto the positively charged proton? Why do hydrogen atoms pair into molecules and why helium atoms don’t? And did you know that answer to the second of these questions is surprisingly close to the distinction between metals and insulators?

“Think how hard physics would be if particles could think.”

— Murray Gell-Mann

Let us quickly review what we learned about the laws of the quantum world in a previous post. The description is in contradiction with the common sense, yet it is the simplest one we found that has survived all experimental tests. The rules of the quantum game can be summarized in only a few principles to which the particles are fully obedient. As Murray Gell-Mann, a pioneer of the elementary particle physics, pointed out — particles do not think.

Having electrons in our mind, the rules are as follows:

(1) Electrons are better to be thought of as waves rather than point objects. The bigger the magnitude of the wave at a given point, the higher the probability that the electron will be found at that point after someone asks for (i.e. measures) its position. These waves propagate in space according to the so-called Schrödinger equation which is very similar to the wave equation — the one that describes the motion of waves on a guitar string or on a surface of a water pond. The most tangible experimental evidence for the wave-like character of electrons comes from the double slit experiment.

(2) The superposition principle says that if an electron can be in one state (let’s call it A) and in another state (let’s call this one B), then it might also exist in a superposition of those two states (something like A + B). Waves on a water pond also have this property, which means that there can simultaneously be several waves moving in various directions on the water surface, each of the waves ignoring all the other. But there is even more to it! The superposition principle means that a single electron can at the same time be in Hong Kong and in Rio de Janeiro — simply because it certainly can be either in Hong Kong or in Rio only. However, if someone measures its position, the electron will randomly choose to be in one of the cities.

(3) How to deal with momentum in the quantum world? Let’s make an analogy with position. A typical electron wave extends in space, therefore the electron doesn’t have a well-defined position. There is, however, a special kind of waves that are very narrow in space. Such waves correspond to electrons with a well-defined position. Similarly, an electron possesses a “sharp” value of momentum only for certain special waves and a “smeared” value for all the other waves. The special waves that carry well-defined momentum are just the ordinary sine waves. The shorter the wavelength, the higher the momentum of the electron. The “average” value of momentum of a general electron wave can be estimated by the typical size of the ripples of the waves. The narrower they are, the bigger momentum is carried.

(4) We can make a similar statement about energy of an electron. A general electron wave does not have a well-defined energy. There are, however, some special waves that carry a “sharp” amount of energy. These are the standing waves and they convey all information about the physical properties of the studied system. For example, the standing electron waves in a hydrogen atom are labelled as 1s, 2s, 2p etc. and they are widely used to describe chemical properties of molecules.

(5) Besides behaving like waves that move in space, electrons also carry a property called spin. At our level of discussion the meaning of spin remains unclear. We just accept as a fact that the spin of an electron can have two opposite values. No more!

(6) The exclusion principle says that two electrons cannot simultaneously be in the same state. There can be at most two electrons wobbling as the same wave, e.g. as the 1s orbital of hydrogen atom, but then they are forced to have opposite values of spin.

These listed principles were discussed in the two previous posts. Now we will add one more: How to calculate the energy of an electron wave?

Consider as an example the hydrogen atom. It resembles a miniature solar system. The heavy proton attracts the lighter electron in a similar way as the heavy Sun attracts the lighter Earth. The mechanical energy of the Earth has two contributions. First, the kinetic energy proportional to the square of Earth’s orbital velocity. Since we can express velocity as the ratio of momentum and mass, we can equally well say that the kinetic energy is proportional to the square of Earth’s orbital momentum. Second, the potential energy in the gravitational field of the Sun. The closer the Earth happens to be to the Sun, the lower is its potential energy. And vice versa, energy is needed to move up in a gravitational field. Everyone who has ever hiked in mountains knows this. (By the way, the Earth really changes its distance from the Sun by about 3% during every orbit. This, however, doesn’t have to do with summer and winter. The Earth comes nearest to the Sun in January.)

One could find the energy of an electron in hydrogen atom in the same way if only electrons were point particles. But they are not. An electron is a wave extending all around the proton, so the distance (and hence also the potential energy) is not well defined. One more step in the calculation is necessary — we have to calculate potential energy at each point of the wave and average it. More precisely, we have to find a weighted average where the “weight” corresponds to the magnitude of the wave. It is like calculating the final grade from a math class in high school: The big tests have more impact on the final grade than the small ones. In the same way the parts of the wave with a large magnitude have more impact on the average potential energy.

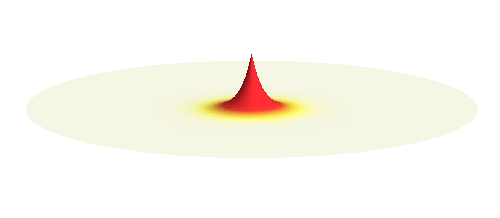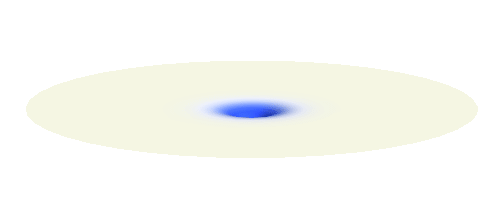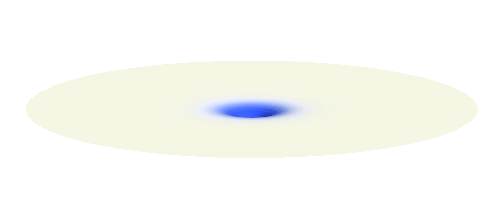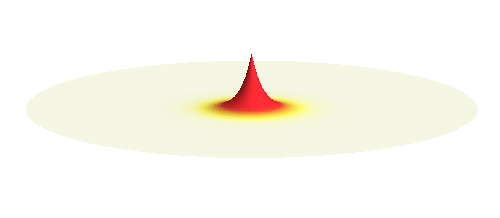
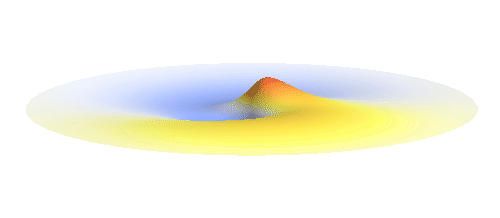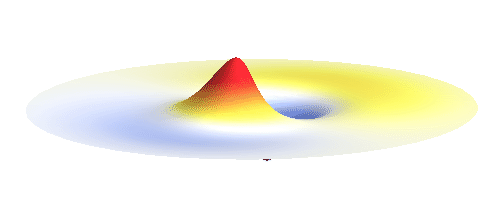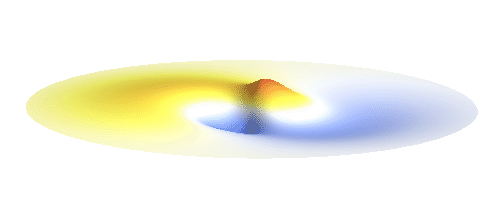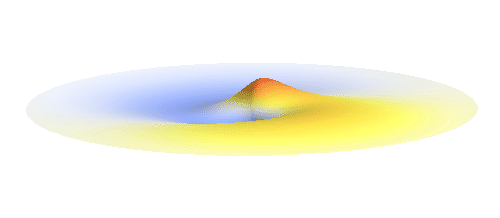
The kinetic energy in the quantum world remains to be proportional to the square of the momentum. Since (see point (3) above) momentum is in general not a sharp-valued quantity, neither is the kinetic energy. However, even if both the potential and the kinetic energy are not well-defined quantities, their sum can be! This happens if the local curvature of the wave (i.e. how wavy it is around a given point, this corresponds to momentum) at every distance is such that we get the same sum of potential and kinetic energy everywhere. Such waves can be found. They are the standing waves discussed above (in point (4)). To get a better impression consider the 1s orbital illustrated below. It has a large curvature (large kinetic energy) near the center, and it is relatively flat (small kinetic energy) on the outside.

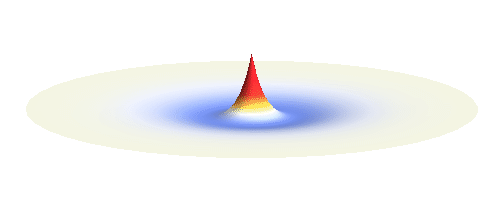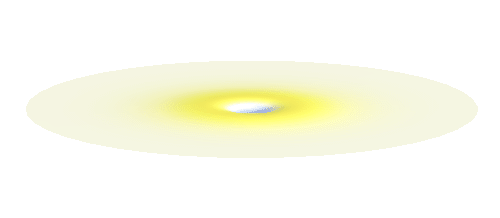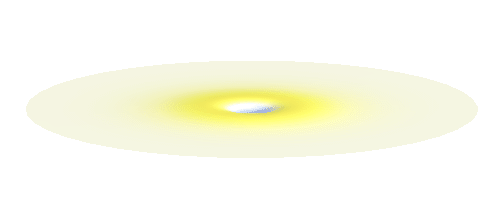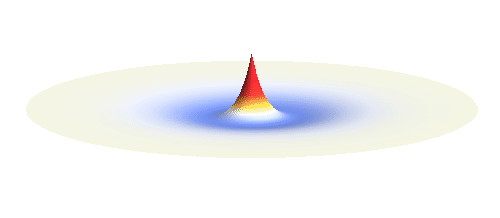
Why doesn’t the electron in a hydrogen atom fall onto the proton? They are attracted by their opposite electric charge so the electron wave should try to get as close to the proton as possible to minimize the potential energy. However, such a narrow wave is very spiky, which means that it has a large momentum and therefore also a large kinetic energy. What is good for one is not good for the other. In its quest to minimize its energy the electron finds a delicate balance when it surrounds the proton in just the right way. Squeezing the electron into a smaller volume would increase the kinetic energy too much, while extending the electron wave to outer space would be too bad for the potential energy. The balance between the two is the 1s orbital pictured below.

Now we get to the interesting part. Why do hydrogen atoms pair into molecules? What happens when two hydrogen atoms are brought close to each other? This problem is not an easy one. In fact, physicists have to use delicate numerical techniques to precisely describe the formation of the bond. But it is easy to grasp the main reason why the atoms bind. They want to decrease the energy of the system. To understand what is going on we will first make a seemingly scary approximation: That the two electrons do not feel each other and the two protons also do not feel each other. The attraction between the electrons and protons are the only forces in such simple system. The effect of the repulsive interactions will be taken into account afterwards.

Consider a hydrogen atom with an electron in the lowest energy 1s orbital and another proton (without an electron) somewhere at a distance. The electron wave is concentrated around its proton but it also has a far-reaching tail. As the second proton gets closer to the atom, the electron begins to feel it and can literally “leak out” to it. But when the electron wave has already leaked out to the other proton, there is also a possibility to leak back to the original proton. The electron wave leaks back and forth in a complicated manner. Such “leaking wave” is around both protons at the same time, but it is not suitable for a good physical description. For that we need to find a standing wave.

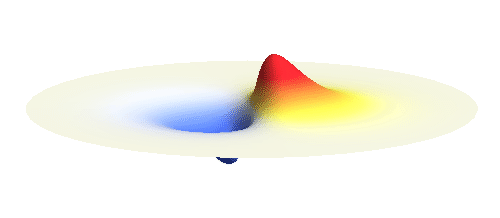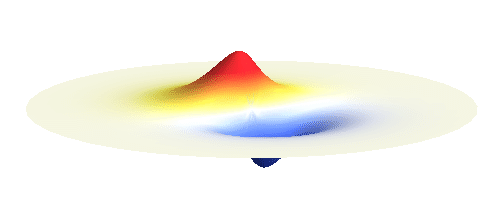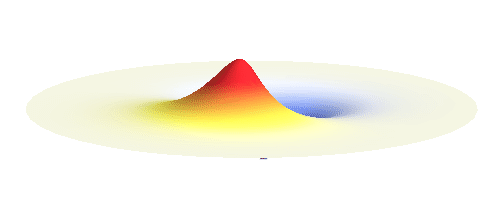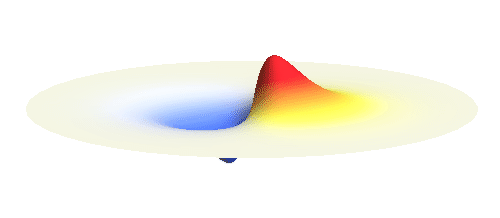
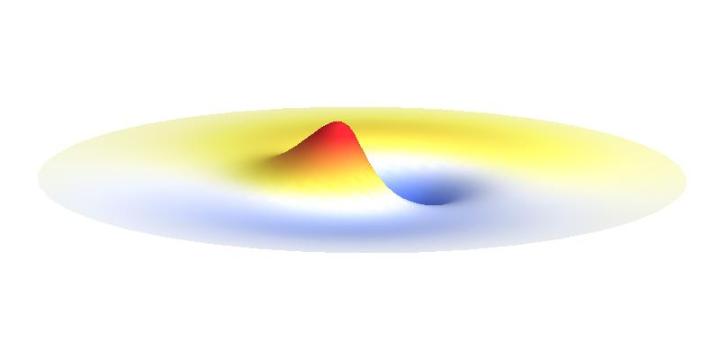
We can get the standing wave with a trick — the superposition principle! What about an electron wave which is partly the 1s orbital of one proton and partly the 1s orbital of the other proton? Indeed, in such case the leaking from the first proton the other compensates the opposite process! This state, also called the bonding orbital, is illustrated in the following animation.

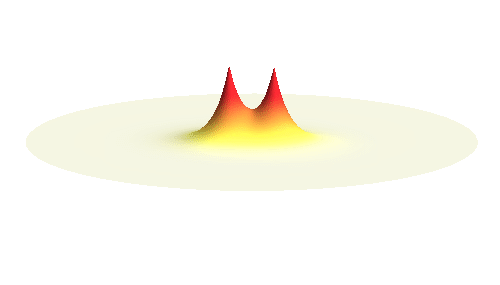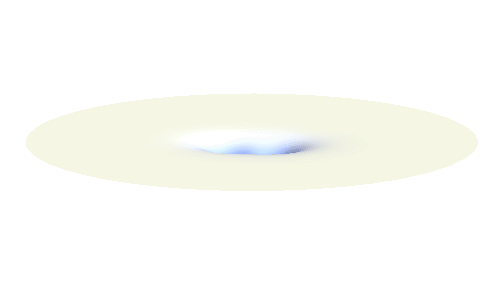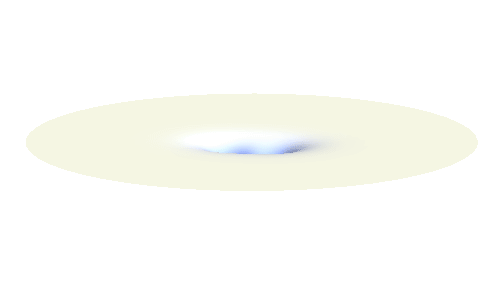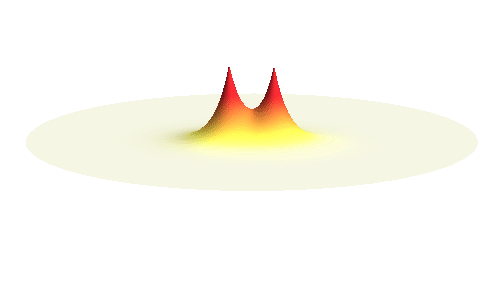
Notice that in this state the electron spends a lot of time between the two protons thus effectively decreasing its potential energy. The shape (or curvature) of the this wave is very similar to that of a single 1s orbital so the kinetic energy is not changed significantly. Therefore the total energy of the electron is lower than it was in a single atom.

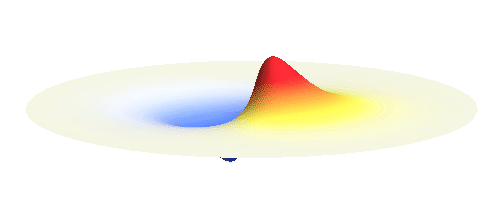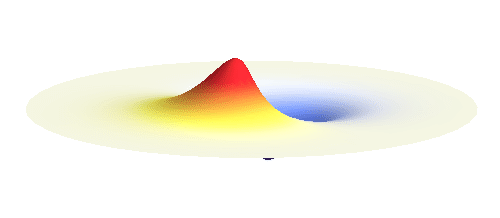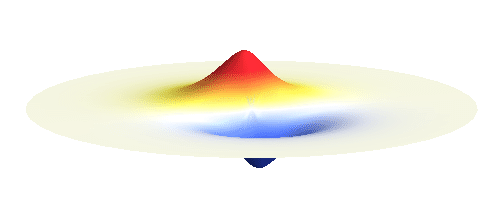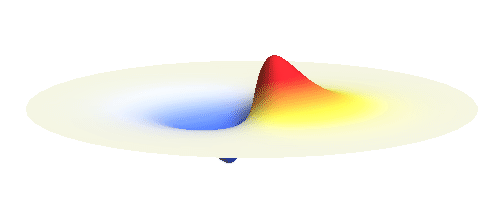
Note that there is also one more possibility to combine the two 1s waves into a standing wave — when they oscillate out of phase. However, in such case the magnitude of the wave between the two protons is suppressed and the electron does not decrease its potential energy effectively. This wave is called antibonding orbital, suggesting that it does not help in creating the bond between the hydrogen atoms.

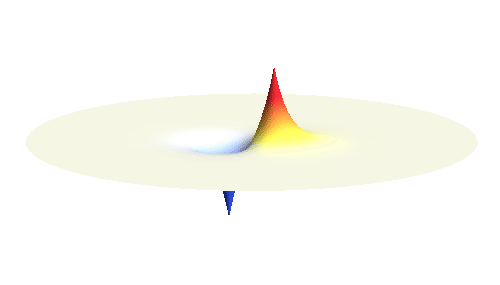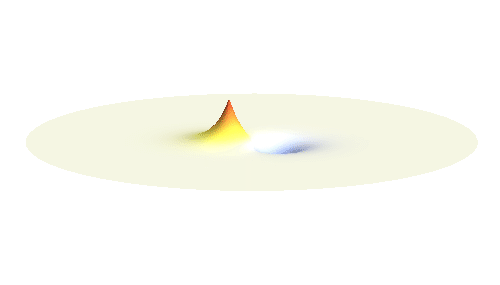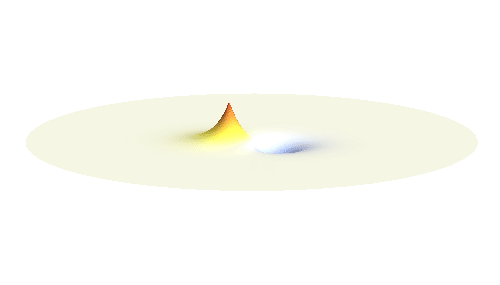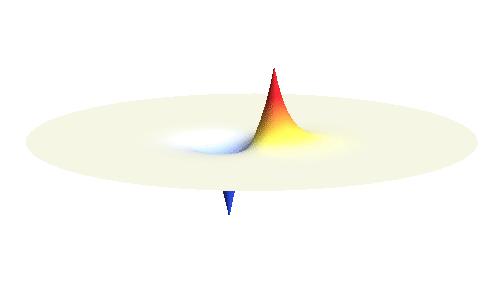
If the atoms are relatively far from each other, the description given above is good enough. But when the atoms get too close to each other, nasty things begin to happen: The positively charged protons begin to feel each other and start to repel strongly. A balance has to be found when the protons are close enough for the electron to take advantage of the extra positive charge, and when they are still sufficiently far apart to keep their mutual potential energy low. Subtle calculation reveals that the optimal distance of the two protons is 53 picometres.

By now we considered two protons with only one electron, together forming an H2+ ion. However, the real hydrogen molecules are electrically neutral, i.e. they have two electrons. Here, the existence of spin comes in useful. Both of the electrons can lower their energy by going to the low energy bonding orbital provided that their spins are opposite. Simple, isn’t it?

Not quite. The repulsive interaction between the two electrons increases the repulsion between the two atoms. Subtle calculation reveals that the optimal distance between the two atoms in a neutral molecule is slightly larger (74 picometres) than in the ion. But there is still an energy gain in forming the molecule.

If you think about it, the conclusion is strange. We started with two neutral objects, each composed of an equally large positive and negative charge. How did it happen that the attractive force between them is stronger than the repulsion? Where did the asymmetry come in?

The answer lies in the wave-like character of the electrons. If an experimenter measures positions of the two electrons, he finds that the electrons avoid each other. If one is between the two protons, the other would be somewhere at a distance. Only very rarely would he find that the two electrons happen to be near each other. In this way the wave character of the electrons allows them to decrease their potential energy — something that the protons cannot do. The formation of the bond is an entirely quantum mechanical phenomenon and cannot be explained using classical analogues.

The results we have discussed are sometimes summarized using the following diagram. Here, the “height” of the states (the horizontal black lines) denotes their energy, i.e. high position means high energy and vice versa. The left and the right column represent the electron states in a single hydrogen atom, and the central column the states in a hydrogen molecule. Arrows represent electrons (with spin) occupying some of those states. Because both electrons have lower energy in the molecule than in a single atom, formation of the molecule is favorable.

Why don’t helium atoms helium atoms pair into molecules? One can draw an analogous diagram for helium. Because the bonding orbital is already occupied with both spins, the extra electrons have to go to the higher energy anti-bonding state. This is too costly, so helium atoms rather stay apart from each other.

The same kind of reasoning can be used to explain formation of other diatomic molecules like O2 and N2, and also of more complicated molecules. The technique we discussed is called linear combination of atomic orbitals (LCAO). Surprisingly, very similar reasoning explains why some crystals (like ice, kitchen salt or diamond) are insulating, while others (like aluminium, iron or indium tin oxide) conduct electricity. We will study this interesting question in the next post.

The pirouette of electrons

“Everything we call real is made of things that cannot be regarded as real. If quantum mechanics hasn’t profoundly shocked you, you haven’t understood it yet.”

— Niels Bohr

“What’re quantum mechanics?”

“I don’t know. People who repair quantums, I suppose.” 

— Terry Pratchett, Eric

 

The Moon orbits the Earth, both the Moon and the Earth spin around their axes, and they jointly revolve around the Sun. So do the other moons and planets in the Solar System. This cosmic ballet is completed by the rotation of the Solar system around the center of the Milky Way. But does this dance also extend to the world of the small? We will see that it does though the steps of the microscopic dance have slightly different rules. In classical physics, the stage of our everyday life, rotation of an object is described by a vector quantity called angular momentum. The direction of this vector is given by the axis of rotation and the right-hand rule, while its magnitude is proportional to the inertia of the body and the rate of the rotation. To give a few examples, angular momentum that describes the Earth’s revolution around its axis points along the North Pole, and the motion of the Earth around the Sun is described by a vector pointing perpendicular to the plane of the Earth’s orbit. A more elaborate example is given by a suspended pendulum: Its angular momentum is perpendicular to the plane of the oscillations and its changes magnitude and direction as the pendulum swings back and forth.

In the world of the small, electrons move around the atomic nuclei in a way somewhat resembling a microscopic planetary system, so we expect the notion of angular momentum to be applicable for them too. However, electrons are waves so we should not be surprised to find some differences from the classical physics. We will discuss the problem in two parts: We will start with the orbital angular momentum (corresponding to Earth’s motion around the Sun) and will afterwards continue with the spin (corresponding to Earth’s spinning around its axis).

The orbital momentum of a single electron is minute and it is typically expressed in multiples of ħ, the Planck constant. This alone is not an extraordinary observation since electrons themselves are very tiny. The remarkable facts are that (1) the orbital momentum is quantized, i.e. its value can be only an integer multiple of the Planck constant, and (2) that due to the uncertainty principle the electron can have only one well-defined component of the orbital momentum vector at a given time. Whoa?! Just wait, we are actually able to understand both of these!

Let us start with two examples that are easy to swallow. The following two animation describe two possible electron waves (they are the p_x + i*p_y and the p_x – i*p_y orbitals, only real parts of the waves are shown) that carry a well-defined angular momentum along the vertical axis, specifically one Planck constant and minus one Planck constant, respectively.   The obvious observation is that motion of these waves is just a uniform rotation around the vertical axis. Clearly that must be why they carry angular momentum along that axis. It sounds very plausible. However, it is not the complete truth. The following electron wave (it is a combination of 2p and 3p orbitals) oscillates in a more difficult pattern, but it has a well defined angular momentum too. Actually, we can determine the angular momentum just from a static image of the wave and the rule is surprisingly easy. Consider the following snapshot of the wave animated above. Notice especially that this wave changes to “minus itself” when rotated by 180°, i.e. one half of the full rotation. More precisely, if you examine the values of the wave along a circle of arbitrary radius, you would find that it has a sine profile! This is illustrated be the green lines in the next figure. Closer inspection indeed reveals that the vertical displacements of these circles along their circumference are perfect sine waves. That is the crucial point and we can understand it by comparing to the ordinary linear momentum discussed in the previous post. There we mentioned that a freely moving electron is described by a sine function, and that direction of that sine wave corresponds to the direction of the electron’s motion. In the case of angular momentum the electron just moves in a circle, so the sine-wave curls in a circle. That’s all there is to it.

We also mentioned that the larger the momentum the shorter the wavelength of the sine function. But in the case of angular motion there is a constraint that the wave must return to its original value after a full 360° rotation. This means that we can only stack an integer number of sine waves around the circle. It can be calculated that one sine wave corresponds to angular momentum ħ, i.e. one Planck constant, two sine waves to 2ħ, three sine waves to 3ħ and so on. If the function does not depend on angle at all, its orbital momentum is zero. Voilá, we have derived the orbital momentum is quantized! By the way, according to this, a wave with angular momentum nħ transforms into “minus itself” after rotation by 360°/(2n). We will return to this point of view when we discuss the spin.

Now to the second mystery: Why can an electron have only one well-defined component of the orbital momentum vector? This is more challenging to illustrate with a single picture but let us try. If you find the discussion too abstruse, just skip the following three paragraphs.

When speaking about sine waves, physicists often use a word “phase” to specify a position within the sine-profile. One period of a sine wave corresponds to 2π, half-period to π, quarter of the period to π/2 and so on. Let us consider an electron wave that has a well-defined z-component of angular momentum 2ħ. Such wave consists of two sine profiles curling around the center or, in our new jargon, to phase 2 x 2π = 4π. This is indicated by the green labels in the figure below. Now, if the wave also had a well-defined angular momentum around the x-axis, the wave would have to change its phase by some fixed amount if rotated by 180° about the x-axis. However, as indicated by the orange arrows, the wave changes phase by 0 somewhere, by π somewhere else and clearly by any other amount in between the two selected points. This is a contradiction: The x-component of angular momentum cannot be well-defined if the z-component is. The phase can increase uniformly around one axis only. Q.E.D. (A remark for those who actually had some course on quantum mechanics: The existence of the contradiction is the essence of the fact that a commutator of two components of orbital momentum is non-zero. By the way, there is a single exception to the contradiction: The components can be all well-defined if they are all zero.)

Orbital momentum is encoded in the electron wave and we understand it fairly well now. What about spin, i.e. the analogue of Earth’s rotation around its own axis? Indeed, an electron can spin around its axis too! However, this spinning is described by an extra variable (called prosaically as “spin”) which is beyond the electron waves that we have discussed by now. For a given electron wave, the spin can be in various possible states. The two properties are completely independent of each other.

Electrons are objects without internal structure or size, so what is the meaning of the spin? Sadly, this question is too difficult to be answered at our present level, especially because special theory of relativity is involved in the explanation. Indeed, this is how D. L. Goodstein remembers asking a very related question the famous Richard Feynman (taken from his book Feynman’s Lost Lecture):

“Feynman was a truly great teacher. He prided himself on being able to devise ways to explain even the most profound ideas to beginning students. Once, I said to him, “Dick, explain to me, so that I can understand it, why spin one-half particles obey Fermi-Dirac statistics.” Sizing up his audience perfectly, Feynman said, “I’ll prepare a freshman lecture on it.” But he came back a few days later to say, “I couldn’t do it. I couldn’t reduce it to the freshman level. That means we don’t really understand it.”

We will not discuss the meaning of spin here. However, we can still spell out some of its characteristics!

First, possible magnitudes of spin are quantized. Contrary to orbital momentum which can have only integers values, spin can have also half-integer values i.e. 1/2, 3/2, 5/2 and so on.

Second, magnitude of spin of fundamental particles is fixed. For example electrons and quarks have spin 1/2, while photons have spin 1. The spin of composite particles is the sum of the spins of its constituents plus an orbital contribution if the constituents revolve around each other. The net spin then depends on the “architecture”. For example, a proton and a neutron are both composed of three quarks and their architecture leads in both cases to spin 1/2. There is also a spin 3/2 version of protons and neutrons that have a different architecture, but they are extremely unstable and fall apart in about 10^(-23) seconds. They are called delta resonances. Rather surprisingly, deducing the actual architecture of a proton is not easy at all!

Third, the spin degree of freedom can be in (2n+1) different states. For electron we have n = 1/2 so we count 2*(1/2) + 1 = 2 different states. They are usually referred to as “up” and “down”, but they might equally well be called “left” and “right” or (to cause as little confusion as possible) as “chocolate” and “banana”. We will discuss this subtlety in a later blog, for now just keep the number “two” in your mind. Another peculiarity is that (according to a description above) spin 1/2 transforms into “minus itself” after rotation by 360° and it only transforms back to itself after two full rotations! This is an observable effect and we will have a closer look at it when we discuss effects of magnetic field.  Unexpectedly though, there are also classical systems that map to themselves after two full rotations and not after just one, see e.g. the Dirac’s belt trick.

We complete our list with the fourth and very consequential characteristic: The classification of particles into so-called fermions (spin 1/2, 3/2, 5/2 and so on) and bosons (spin 0, 1, 2 and so on) which describes properties of a system of several particles. The first group is characterized by the Pauli exclusion principle stating that any two fermions must necessarily be in different states. There is no such restriction for bosons.

The consequences of the exclusion principle are far-reaching, the most prominent example is certainly the periodic table of elements. In their quest to minimize the energy, atoms tend to be neutral i.e. they contain the same number of electrons as there are protons in their nuclei. But electrons are fermions and due to exclusion principle they cannot all occupy the lowest energy state — the 1s-orbital. They are forced to occupy the other orbitals with higher energy. They are like bulls fiercely pushing each other away from their territory. To be more precise, a given orbital (i.e. a standing wave as introduced in the previous post) can contain at most two electrons — one with  spin “up” (or “chocolate”) and one with spin “down” (or “banana”) — and nothing more. But the “other orbitals” have ever different symmetries and energies thus leading to a multitude of different chemical properties. Were there not the exclusion principle, all the electrons would collapse to a single state, and all atoms would be equally dull. The exclusion principle makes our world an interesting place to live in! The exclusion principle also acts on a more grandiose scale. After a star the size of the Sun burns all its hydrogen (and after a relatively brief period of being a red-giant)  it shrinks to a small (approximately the size of the Earth) and very dense object called a white dwarf which is stable again. What prevents a white dwarf from further contraction is the exclusion principle. The star’s electrons relentlessly protect their territories. The gravity can overcome the electric repulsion, but not the unyielding exclusion principle. In an even more massive star the positively-charged protons and negatively-charged electrons merge under pressure together into electrically neutral neutrons. Such star shrinks even more (to roughly 10 km radius) and is then called a neutron star. It maintains stability via the exclusion principle again, the only difference is that now the bulls are the neutrons!

In the next blog we will introduce one of the most central notions of the material physics called the Bloch theorem. When we put this theorem together with the Pauli exclusion principle, we will understand why some materials are metals and other are insulators. By the way, in certain materials electrons of opposite spin can bond into pairs (called the Cooper pairs). These have spin 1/2 + (-1/2) = 0, i.e. the pairs are bosons. The consequences are striking. Zillion of these bosons can literally condense into a single wave which can then move through the material with a completely zero electrical resistance. This phenomenon is called superconductivity and we shall have a closer look at it later as well.

Sailing the waves of probability

Consider the subtleness of the sea; how its most dreaded creatures glide under water, unapparent for the most part, and treacherously hidden beneath the loveliest tints of azure.

— Herman Melville, Moby-Dick; or, The Whale

Erwin with his psi can do
Calculations quite a few.
But one thing has not been seen:
Just what does psi really mean?

— Erich Hückel’s unpublished poem

You may find the mathematical formulation of mechanics abstruse, but all of us intuitively understand how it works. You know that you have to run fast for bus if you leave home too late, you understand why objects cast longer shadows at sunset than they do at noon, and you commonly use a lever to lift objects that are otherwise to heavy to be moved. The evolution has shaped us to understand velocities, angles and forces. We are all physicists at heart. But we are classical physicists and our intuition fails us when we encounter the world of the small.

 

Quantum mechanics is based on a handful of postulates. They are strange, but they are rigorously formulated and they passed all experimental tests ever devised  so they have to be accepted as such. In the following text we will discuss some of them. To avoid ambiguity I will discuss an electron, but you should keep in mind that these laws apply to all the particles down there.

You have certainly heard about at least some of the strange conclusions of quantum mechanics, like “an electron can be at several places at once” or that “we cannot measure the position and velocity of an electron at the same time“. These statements are true and indeed odd. But they are much less perplexing if we accept one experimental fact: Electrons are not really point-like particles. They are better to be thought of as waves. These waves occupy some finite region of space as a cloud does, and as well as a cloud these waves do not have sharp boundaries. A typical extent of these waves is usually microscopic. In fact, it is the extent of these electron waves that defines the size of an atom.

To appreciate the idea of an electron wave, we have to address two questions. First, what is the evidence that they really are waves? And second, how does this waviness mitigate those baffling claims mentioned above? Let us start with the experimental question. Though the concept of an electron wave had been around since de Broglie proposed it in 1924 to explain properties of emission spectra of hydrogen, it became much more tangible and inescapable after an experiment performed by Claus Jönsson in 1961. His experiment was voted “the most beautiful experiment” by the readers of Physics World in 2002. He brought the world of the small much closer to us. But to explain its consequences we have to return to the beginning of 19th century when a far-reaching discovery happened in another field of physics — the study of light.

Since the time of Isaac Newton and Christiaan Huygens there had been a discord in the physics community about the character of light: Is it made of particles or waves? After more than a century, Thomas Young resolved this dispute by performing an experiment presently known as “the double-slit experiment”. The setting was easy. Consider the propagation of light from a light bulb to a wall and also some objects standing in the way. That’s all Young had to study to reach his conclusion. He just used a very special object as an obstacle — a dark foil with two parallel narrow openings. The “double-slit”.

You probably visualize light moving in straight lines (the light rays) so you understand why objects standing in the way cast shadows on the wall. If the light bulb is very tiny, all rays leave the bulb at more-or-less one spot and you expect the shadows to be sharp. This is what the Newton’s particle theory predicts: The particles of light move in straight lines unless an object stands in the way. On the other hand, the prediction of Huygens’ wave assumption is different. Waves can change direction of motion when they pass by a corner. For example, when you are playing outside, you can hear people chattering and a car engine running on the other side of a building in spite of the fact that there is no straight line connecting those events to your ear. It works because sound is a wave and it does not propagate in straight “rays”.

So Thomas Young put a double-slit in front of the bulb and looked at the shadow. And, lo and behold, he didn’t see two bright strips. Instead he observed a multitude of bright and dark strips! This contradicts the particle theory, while the wave theory has no troubles to explain it. The phenomenon is called wave interference. It is a bit awkward to be described in words so I urge you: Please watch this neat video where wave interference is demonstrated with both light and water waves. (An important remark: The reason that we do not perceive the wave character of light in our everyday experience is its minute wavelength — about one hundredth of the thickness of your hair. In Young’s experiment the two slits have to be very close to each other.)

Now let’s move back to 1961. Claus Jönsson did the same experiment with a beam of electrons. He looked at the wall and, voilà, found an interference pattern too! Even more fascinating is that this experiment can be carried out with such weak electron beam that there is at each moment just one electron between the source and the wall. Even then one would still find the interference pattern. This means that every electron is a wave by itself, this wave goes through both of the slits and then interferes with itself. There is really no contradiction. In his celebrated physics lectures Feynman concludes that “the paradox is only a conflict between reality and your feeling of what reality ought to be.” Meanwhile, analogous experiments have been performed with other particles as well, the largest up-to-date being fullerene (1 300 000 times heavier than electron) and a derivative of phthalocyanine (I don’t know what that is either, but it is 2 400 000 times heavier than electron).

Erwin Schrödinger, the guy mentioned in the Hückel’s poem, devised an equation that describes propagation of these waves. From mathematical point of view it is not precisely a wave equation, but it is harmless for us now to regard it as such. So, for example, if you put an electron next to a proton, it can get trapped due to the attractive electrostatic interaction. This has to be viewed as a wave localized around the proton, not leaking to the outer space, and somehow oscillating in time.

An important concept is that of a standing wave which is often explained using an elastic string. In similar way the electron waves can also be “standing”. Do you remember the chemistry class where we denoted various electron states (usually called orbitals) by strange combinations of symbols like 1s, 2s, 2p_x or 3d_xy? They are just labels for all possible standing waves of an electron in a hydrogen atom. The following four animations display the four aforementioned waves in the xy-plane. (Keep in mind that these waves actually oscillate in three dimensions but that is too difficult to fit into your two-dimensional computer screen. A remark for experts: Of course I only plot the real component of the wave.)

Notice also that the frequency of these standing waves is different. The first picture has the longest period, i.e. it oscillates very lazily, while the last one is very dynamic. It turns out that the rate of these oscillations is proportional to the electron energy. Since there is just a discrete set of various standing waves, the electron in this system can possess only certain discretized values of energy. That is a well-known experimental observation that de Broglie originally intended to explain.

Now we must inevitably arrive at two of the postulates of quantum mechanics. First, an actual electron wave can be any combination of those standing waves mentioned above. This is not very surprising since all waves can combine in a similar way. If you listen to an orchestra, all sound waves coming from all the instruments come to your ear combined together and you can perceive all the beauty at once. Waves on a water pond can add together in the same way. This is just what waves do and the electron wave is no exception. A particular combination of 1s and 2p_x orbitals might look like the following animation.

The second postulate is about measurement. This is certainly the most troubling of the postulates. Since electrons are so small, it is not easy to devise an experiment that probes its properties. For simplicity, think of a measurement of energy as asking the electron “Hey, buddy, what is your energy?” upon which it willingly gives some number. When the electron wave is one of the standing ones mentioned above, there is no complication: The electron gives you a number and continues its existence without bothering about you.

However, a complication occurs when the electron wave happens to be a combination of several of the standing waves. A sober person would expect that the electron would tell you some average of the energies of the corresponding waves. But this is not what happens. The electron randomly chooses energy of one of those waves and after the measurement it instantaneously “collapses” into that particular wave. The measurement changes the state of the electron and there is no way to circumvent this problem. It is as if you tried to localize a car by setting a lot of mines on the road, instead of innocently looking at it from a distance. In quantum mechanics every measurement “undermines” the electron leading to a change of its state. This strange characteristic of measurement troubles physicists until today, see e.g. here and here.

What if we ask an electron about its position? Such measurement also changes the electron wave. In this case it instantaneously collapses into a wave that has a well-defined position: A very thin peak localized around some point in space. The probability that the wave collapses into a specific point in space is proportional to the square value of the wave at that point. A quick look at the animations above reveals that the 1s electron is most likely to be found in the center because the wave has its maximum there. On the other hand, the 2p_x orbital is never found in the center because the wave has zero amplitude there. It is the spatial extent of the electron wave why it is sometimes claimed that an electron can be “at several places at once”.

And what happens when we ask an electron about its momentum (i.e. mass times velocity)? This time we have to identify states with well defined momentum. They turn out to be the ordinary sine waves with all possible wavelengths and propagating in all possible directions; the first represents the magnitude and the second the direction of the momentum. There is a mathematical theorem (the Fourier decomposition) according to which any wave can be expressed as certain combination of suitably chosen sine functions. The details are technical but we it is feasible to understand it without math. Have again a look at the 1s and 2p_x waves animated above. The peak of the 1s orbital is narrower than the peaks of the 2p_x orbital. This means that the first will be well fitted by sine waves with smaller wavelength than the second. Smaller wavelengths mean larger momentum. (Do you remember that light with short wavelengths is more energetic and carries more momentum? The same statement holds for electron waves.) This means that 1s electrons move on average faster than 2p_x electrons.

We can finally address the almost mystical uncertainty principle. The electron cannot have a well-defined position and momentum at the same time. The first requires the electron wave to be peaked at tiny extent of space, while the second requires it to be an extended sine function. These two conditions are clearly incompatible. This is the essence of the Heisenberg’s uncertainty principle.

It is possible to make a compromise between position and momentum that is called a wave packet. In that case the electron is not located at one spot but is spread in a wider “packet”. The packet has a sine-function profile but its amplitude decays away from the middle. This is the kind of wave you have to consider in the double-slit experiment. A typical wave packet is shown below.

Now you can visualize a particle in the Wonder World. But can we also visualize several particles in the same way? As mentioned in the previous post, a typical number of particles in a typical object is mind-bogglingly huge, so the question is important. We will see in two weeks that we can do so if we adopt one extra rule. This rule comes in two variants depending on the particle species. We will see that the rule that applies for electrons easily explains why there are so many elements in the periodic table, and also why some materials are insulators while other are metals. The second variant applies e.g. for helium atoms and it explains their superfluid phase characterized by zero viscosity flow. We will get to these phenomena soon!

Building up a Universe

In that far distant age there lived, as there had always lived, a god named Chaos. He was all alone, and round him there was nothing but utter emptiness. In those times there was neither sun, nor light, nor earth, nor sky. There was nothing but a formless void and thick darkness stretching to infinity.

Untold centuries rolled by like this until, at last, Chaos grew tired of living by himself. It was then that he first thought of creating the world.

— Greek Mythology, The Birth of the World

There is a theory which states that if ever anyone discovers exactly what the Universe is for and why it is here, it will instantly disappear and be replaced by something even more bizarre and inexplicable.

There is another theory which states that this has already happened.

— Douglas Adams, The Restaurant at the End of the Universe

Many physicists are very passionate about the search for the Theory of Everything. This means identifying the basic building blocks of the Universe and quantifying the interactions between them. Our concepts of these have evolved rapidly over the course of history. Most importantly, as we have entered the scientific age, the generally accepted view of the Universe has become based on experimental evidence rather than on unjustified beliefs. It is not claimed anymore that all substances in the world are made of a mixture of the Aristotle’s elements (i.e. fire, water, earth and air). It was experimentally revealed that things around us are made of atoms, and that these atoms are composed of yet smaller constituents: electrons, protons and neutrons. Even more recently it was discovered that protons and neutrons are made of even tinier particles called quarks. Presently, a lot of people hypothesize that the fundamental building blocks of the Universe might turn out to be some miniature vibrating strings. I have to confess that I, too, share this passion for the understanding of the Universe.

Unfortunately, many researchers go too far in this reductionistic view of the world. They claim that the Theory of Everything, once identified, will explain all other phenomena, thus degrading the rest of science into plain engineering problems. While visiting CERN as a student in 2010, I attended a popular lecture where the speaker really claimed that the Theory of Everything explains the rest of physics, that physics in turn explains all the chemistry, that chemistry explains all the biology… all the way up to sociology and politics. But our understanding of the world does not support this claim. Deducing complex phenomena from the underlying laws turns out to be at least as intellectually demanding as the search for the Theory of Everything itself. And breathtakingly beautiful too, as is obvious after seeing the subtle machinery within each living cell of every living organism. The fundamental laws are hardly helpful in explaining the beauty that surrounds us. I have the luck to work in a field of science where this happens and which is sufficiently mathematical to articulate some of the ideas more rigorously. It is the study of materials, also called condensed matter physics, and the argument was immortalized in Phil Anderson’s essay More Is Different.

In condensed matter physics we have our Theory of Everything. (Or should we better call it the Theory of All Materials?) It is the theory of atoms. An atom can give off a negatively charged electron to become a positively charged ion. The electrons and ions interact electrically and magnetically. We can also quantify their energy of motion. This all has to be described within the well-established framework of quantum mechanics. Understanding the details is not an easy duty at all. Anyway, the important point here is that we know the underlying theory exactly. Of course there is a more fundamental theory which explains the properties of the atoms (e.g. their masses) but for our purposes we can simply measure them and take them for granted. Yet, knowledge of this Theory of All Materials has not led us to a complete understanding of all materials, and there are still major discoveries being made in the field. As Bob Laughlin and David Pines put it: “Theory of Everything is not even remotely a theory of every thing”

The main obstacle to predicting properties of a typical material is the monstrous number of particles it is composed of. There are about as many atoms in your lunch meal as there are stars in the entire observable Universe. (This estimate is surprisingly close to the Avogadro constant.) Because of the arcane aspects of quantum mechanics we can hardly calculate properties of more than about one hundred atoms. Unfortunately, there is a huge difference in the behavior of 100 atoms and 100 000 000 000 000 000 000 000 atoms (size of your lunch meal). For example, you know that water freezes when you cool it below 0 °C  (32 °F), this transition being remarkably sharp. On the other hand, a ‘nanodrop’ of water composed of only one hundred water molecules would freeze into ice only very lazily over a wide range of temperatures. Instead of a sharp transition from liquid to solid, one would observe a smooth crossover from one phase to the other without clear distinction of the two. For small systems, the notion of a phase transition ceases to have a meaning.

There are two nontrivial kinds of phenomena that can occur in a large aggregate of atoms. We call these phenomena emergent to stress that they are not inherent properties of the constituent atoms. First, new phases of matter can appear. Second, new kinds of particles can appear as well. Both of these statements might cause confusion so let me explain more carefully.

By phase we mean any organizational pattern. Atoms in a crystalline solid are organized in a different pattern than they are in a liquid or a gas. But we extend the notion of a phase beyond these three standard examples. A magnet is a new organizational pattern, conductors and insulators differ in the organizational pattern of their electrons. Similarly we can argue for liquid crystals (you have them in the LCD of your laptop), superconductors (materials with zero electrical resistance, they are often used to generate large magnetic fields), Quantum Hall states (utilized for the most precise measurements of electron charge e and Planck constant h ever performed), topological insulators (hypothesized to be the future materials for computer processors), superfluids (the strange phase of Helium), supersolids (an even stranger phase of Helium) and many others. Just don’t panic, we will get to all of these exotic things in the later posts. My point here is that there is a common feature to all of these phases — they can’t be derived from the theory of atoms.

The second emergent phenomenon is an appearance of new particles in the material. This is a bit inaccurate. In fact, there is nothing really new — only the electrons and ions. However, when a material transforms into a new organizational pattern (e.g. it crystallizes), the electrons and ions will tend to move collectively (e.g. as vibration modes moving through the crystal). Moreover, the laws of quantum mechanics force these collective motions to carry quantized value of energy. Just like light is composed of photons (from Greek photo-, meaning light) , each one carrying certain amount of energy and indivisible into smaller parts, it turns out that sound waves (vibrations) in a crystal also come in indivisible bits. We call them phonos (from Greek phono-, meaning sound).

There is a big difference between photons and phonons. While a photon is considered to be a fundamental constituent of the Universe, a phonon is not — it is just a collective motion of many atoms. Yet, there are experiments in which phonons appear to be perfectly real. A good example are the so-called scattering experiments: If one shoots tiny particles, e.g. neutrons, into a material, they can get scattered. That means that they change their velocity and direction of motion. But there are certain conserved quantities in physical processes: momentum and energy. Therefore the change in the energy and the momentum of the scattered neutron must be carried by ‘something’ existing in the material. By careful scattering experiments it is possible to probe properties of this ‘something’. Surprisingly, this ‘something’ does not turn out to be an atom nor an electron. It is the phonon. It is this strange quantized collective motion of a multitude of atoms that carries the energy and the momentum of the scattered neutron. Without a microscope it is impossible to see its collective nature. If somehow the course of history would have been different and we would have performed scattering experiments before having discovered atoms, the experimental evidence would compel us to call phonons real. (And the physicists would have helplessly try to understand puzzles like why those particles are trapped inside the crystal and cannot get out.) Indeed, in certain sense phonons are truly real: It turns out to be much easier to study certain properties of materials (e.g. their heat capacity) in the language of phonons, rather than atoms.

Phonons are just one example of a collective motion that can behave like real particles. But there are many other examples, some of them with characteristics very unlike those of the underlying electrons and ions. In certain organizational pattern we found that an electron (bearing spin and charge) can split into two particles, one carrying the spin and the other keeping the charge. In another one we discovered a collective motion that carries one third of the electron charge. In both of these phenomena, all electrons and ions remain whole, nothing gets split. What really happens is that a multitude of electrons starts to move collectively in a pattern that masks their original properties and fools us to observe something unusually strange. I add one final exotic example — a magnetic monopole. You know that if you break a magnet into two halves, each of the halves will have both the North pole and the South pole. However, in the so-called spin ice materials it might be possible to create a collective motion bearing only one of the two poles. Using the words of Alice entering the Wonderland, “Curiouser and curiouser.”

I will conclude with two speculations. The first one: Might this also be the story of the Universe? What if the Universe is actually made of a zillion tiny ‘things’ and all that we perceive as the fundamental particles — electrons, photons, quarks — are actually collective motions of a large number of these ‘things’? What if a photon has an analogous collective explanation to a phonon? There are attempts to explain the Standard Model of elementary particles in this way of reasoning. More recently also gravity began to be suspected of being an emergent phenomenon. These hypotheses will be hard to prove or disprove, since it is hard to propose an experiment that would distinguish them from the standard picture of fundamental physics. However, they might give us a simplified mathematical language and inspire novel ideas for our understanding of the Universe.

The second one: What if this is also the story of ourselves? Might it be that intelligence and consciousness emerge spontaneously in a large neural network in the same way as crystalline solids and magnets emerge in the a vast assemblage of atoms? Here we go beyond the firm ground of established science but there are people who attempt to define consciousness in a rigorous mathematical way. We have to see what the future research will reveal.

Emergent complexity is ubiquitous. A lot of atoms can lead to a new phase of matter or make up a factory called a ‘living cell’. A wisely assembled materials build up a computer, while a large number of cells gives life to a dandelion or a dolphin. Computers and animals are capable of a complex behavior. A large number of people can exhibit further emergent self-organizational phenomena like architecture of cities, social networks and macroeconomics.

In this blog I will introduce you to to the emergent Wonder World of condensed matter physics. I will describe to you some of its recent discoveries and reveal how beautiful they are. We will discuss those strange organizational patterns mentioned above and their potential applications. But before we get there, we must learn the rules of the Wonder World. It is a world of atoms and it is ruled by quantum mechanics. We therefore have to discuss several questions: What is quantum mechanics? Why is it different? And what exactly is “quantum” about it? We will begin this journey in two weeks!